بحث عن الدوال الرئيسة الام والتحويلات الهندسية وامثله

إن بحث عن الدوال الرئيسة الام والتحويلات الهندسية وامثله من شأنه أن يساعد الطلاب على التعرف على ماهية هذا النوع من الدوال، ومن ثم التفريق بينه وبين الأنواع الأخرى، وعبر موقع تثقف سنقوم بعرض نموذج بحث عن الدوال الرئيسة الام والتحويلات الهندسية وامثله جاهز للطباعة.

بحث عن الدوال الرئيسة الام والتحويلات الهندسية وامثله

في حال كنت من محبي مادة الرياضيات، أو كنت من الطلاب الدارسين في المراحل التعليمية المختلفة، فبالطبع يمكنك الاستفادة من الاطلاع على بحث عن الدوال الرئيسة الأم والتحويلات الهندسية وأمثلة توضيحية على العلاقة بينهما.

حيث إن هذا البحث عادةً ما يشتمل على العديد من العناصر والتي تتنوع بين تعريف العلاقة وتعريف الدالة، إلى جانب ذلك فإنه سيتضمن الكثير من أشكال الدوال الأكثر شيوعًا وإليك الفهرس الخاص بالبحث فيما يلي:

اقرأ أيضًا: بحث عن مستويات بناء جسم الحيوان والتركيب الداخلي له

الفهرس

• مقدمة بحث عن الدوال الرئيسة الام والتحويلات الهندسية وامثله.
• تعريف الدوال “الأم” الرئيسة.
• تعريف العلاقة.
• الدوال الأم الأكثر شيوعًا.
• الدالة الثابتة.
• دالة الجذر التربيعي.
• دالة المقلوب.
• الدالة الدرجية.
• دالة القيمة المطلقة.
• التحويلات الهندسية.
• خاتمة بحث عن الدوال الرئيسة الام والتحويلات الهندسية وامثله.

مقدمة بحث عن الدوال الرئيسة الام والتحويلات الهندسية وامثله

إن الدوال الرئيسية هي إحدى المصطلحات الهامة التي يتضمنها علم الرياضيات، كما أن هذا المصطلح عادةً ما يأتي مصاحبًا إلى العديد من المصطلحات الرياضية الأخرى، حيث إنه يتضمن العديد من الأنواع الأكثر انتشارًا.

من خلال هذا البحث الخاص بالحديث عن الدوال الرئيسة “الأم” وعلاقتها بالتحويلات الهندسية، ينبغي أن يتم التعرف على المعنى المقصود من تلك المصطلحات الرياضية، ومن ثم فسيبدأ هذا البحث بالإشارة إلى تعريف الدالة الأم وتعريف العلاقة.

إلى جانب ذلك فسوف نشير إلى بعض التفاصيل حول الدوال الأم الأكثر شيوعًا، والتحويلات الهندسية، كما سنعرض من خلال البعض أمثلة توضيحية على الدوال الرئيسة والتحويلات الهندسية، وينبغي أن ينتهي البحث بخاتمة تعمل على تخليص أهم ما ورد بمحتواه.

تعريف الدوال “الأم” الرئيسة

يشير تعريف الدالة إلى تلك العلاقة التي تربط بين كل العناصر في المجال الواحد، وتجدر الإشارة إلى أن عملية الربط تلك ينبغي أن يحددها مدى معين.

إلى جانب ذلك فإن الدوال لها شكل معين، وتظهر على عدة أنواع، حيث تتنوع بين الدوال المتباينة والدوال الثابتة، بالإضافة إلى تلك الدوال التكعيبية والتربيعية وغيرها من الأنواع الأخرى.

الجدير بالذكر أن مصطلح عائلة الدوال يشير إلى مجموعة من الدوال التي تشترك فيما بينها في صفة واحد أو أكثر من ذلك، كما أن الدالة الرئيسة التي يُشار إليها باسم “الدالة الأم” هي بمثابة أبسط تلك الأنواع.

من ثم فإن هذا النوع السابق الإشارة إليه من الدوال، هو الذي يتيح لك إمكانية إجراء التحويلات الهندسية من خلاله؛ وذلك بغرض التعرف على الدوال الأخرى التي تنتمي إلى باقي العائلة، وإليك فيما يلي صورة توضيحية لشكل هذا النوع من الدوال:

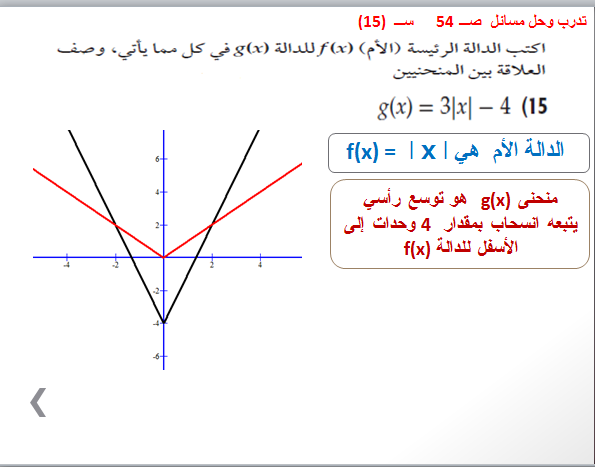
تعريف العلاقة

يشير مصطلح العلاقة إلى الارتباط الذي يجمع بين عنصرين في المجموعة الواحدة، والذي عادةً ما يكون ناتجًا عنه تسمية تلك العناصر بعناصر مجموعتي المدى والمجال.

الدوال “الأم” الأكثر شيوعًا

الجدير بالذكر أن تلك الدوال تظهر على العديد من الأنواع، والتي تتنوع بين الدوال المحايدة والدوال التربيعية، إلى جانب ذلك فإنه توجد الدوال الخطية والدوال المتباينة، أيضًا توجد الدوال التكعيبية والتربيعية.

من ضمن تلك الدوال المنتشرة إلى حد كبير نجد دالة الجذر التربيعي والدالة المحايدة، بالإضافة إلى دالة المقلوب ودالة القيمة المطلقة، كما يوجد دالة أكبر عدد صحيح والتي تعرف باسم الدالة الدرجية.

الدالة الثابتة

ينتمى هذا النوع من الدوال إلى الدوال الخطية، كما أنه أحد الدوال الرئيسة التي تعرف باسم الدوال الأم، كما أن هذا النوع من الدوال له شكل مميز، وإليكم صورة توضيحيه لشكله فيما يلي:

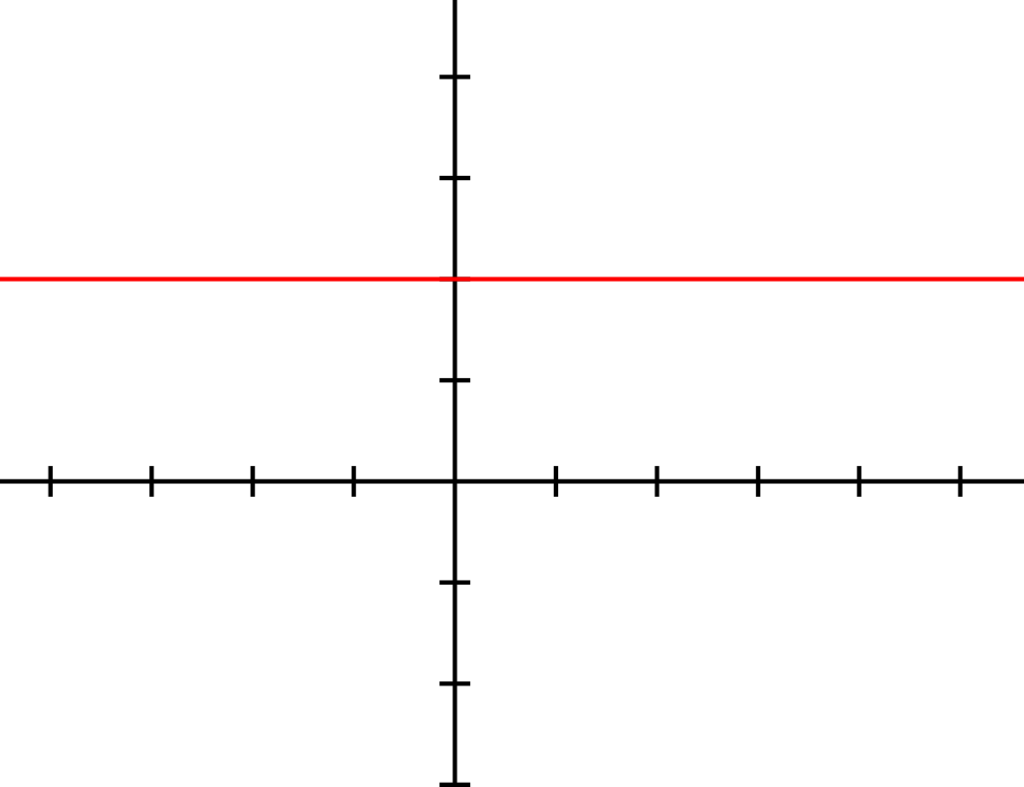
الجدير بالذكر أن مشتق التابع الثابت في هذا النوع عادةً ما يساوي صفر، إلى جانب ذلك فإن التابع الثابت في نظام الإحداثيات الديكارتية في هذا النوع من الدوال يتم التعبير عنه من خلال خط مستقيم، يظهر موازيًا إلى محور السينات.

كما أن هذا الخط المستقيم دائمًا ما نلاحظ كونه يقطع محور السينات، وذلك عند القيمة الثابتة للتابع نفسه وتتم كتابة الدالة على الصورة f(x)=C.

دالة الجذر التربيعي

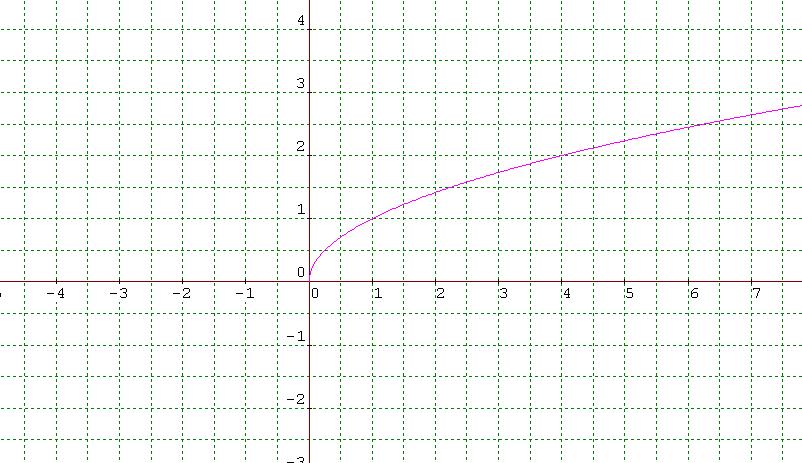
بالنظر إلى الصورة التوضيحية السابق عرضها نجد أن تلك الدالة هي إحدى الأنواع الأكثر انتشارًا، إلى جانب ذلك فإنها من الدوال كثيرة الحدود، والتي يتم الاعتماد عليها في العديد من العمليات الرياضية وتتم كتابة الدالة على الصورة f(x)=√x ويجب أن يكون المتغير x يزيد قيمته عن صفراً.

شاهد أيضًا: بحث عن المتممات المنصوبة والمجرورة

دالة المقلوب

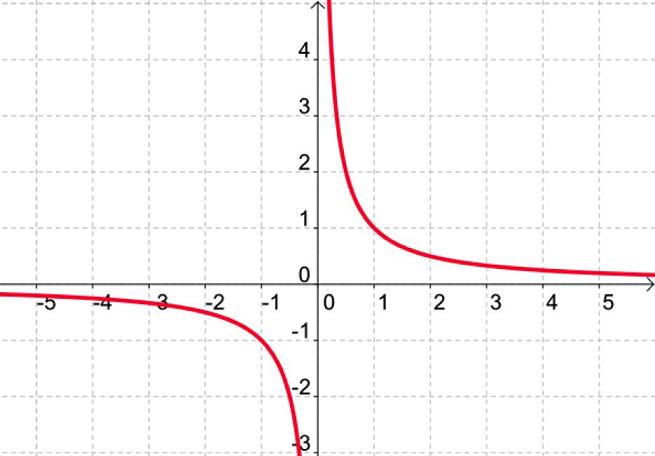
في هذا النوع من الدوال يُشار إلى أنها تلك الدالة التي يتم فيها تحول العدد إلى المقلوب الخاص به، وتجدر الإشارة إلى أن تلك الدالة عادةً ما تعتمد على الشكل التالي:

f(x)=1/x  بشرط أن لا تساوي قيمة المتغير x صفراً.

كما أن لها العديد من الأنواع، ومن ثم فإنها تشتمل على تأليف دالة المقلوب والتكامل، وهي أحد الأنواع الأكثر انتشارًا والتي تنتمي أيضًا إلى عائلة الدوال الرئيسة “الأم”.

الدالة الدرجية

يعرف هذا النوع من الدوال أيضًا باسم دالة أكبر عدد صحيح ، كما أنه يحتوي على محورين أساسيين، وهو أحد الأنواع الأكثر انتشارًا من بين الدوال الرئيسة الأخرى وتتمّ كتابتها على الشكل الاتي:  ق(س)=[س]  حيث تمثل الدالة أكبر عدد صحيح تساوي قيمته أو تقل عن المتغيّر س.

دالة القيمة المطلقة

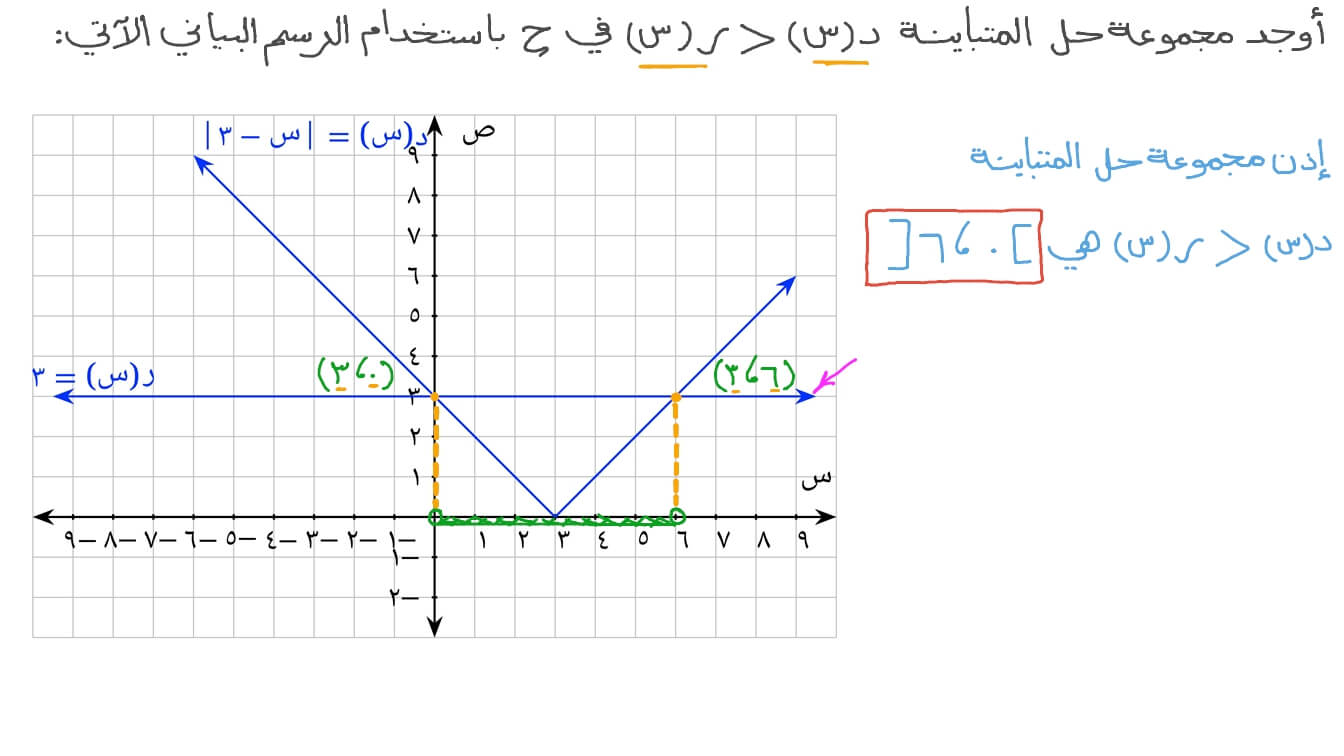
كما أن تلك الدالة يرمز لها برمز| a | ، وفيها عادةً ما تكون القيمة مساوية للصفر أو ذات رقم موجب، ومن ثم فإنه لا يمكن أن تكون قيمة تلك الدالة ذات رقم سلبي على الإطلاق، ولكنها عدد صحيح.

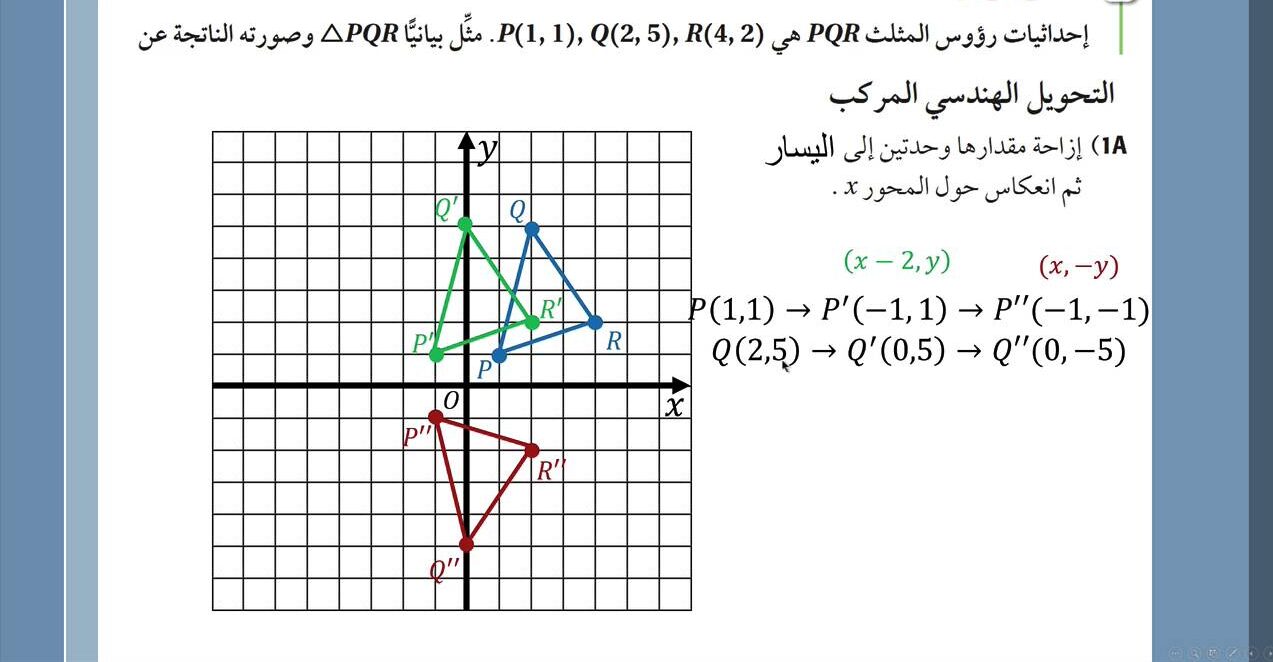
تجدر الإشارة إلى أن مصطلح التحويلات الهندسية من شأنه أن يمتلك بعض التأثير الذي يمكن ملاحظته على شكل المنحنى الذي تظهر بها الدالة الرئيسة “الأم”، إلى جانب ذلك فإن تلك التحويلات الهندسية تنقسم إلى نوعين أساسيين:

• التحويلات غير القياسية: هي تلك التحويلات التي تعمل على تغيير شكل المنحنى، والتي تتمثل في التمدد.
• التحويلات القياسية: يشير هذا النوع إلى التحويلات التي من شأنها أن تُغير موقع المنحنى فقط، وعليه فإنه ليس لها أي تأثير على الشكل الخاص به وأبعاده، ويتمثل هذا النوع في الانعكاس أو الانسحاب.

إليك من خلال الصورة التوضيحية التالية، أحد الأمثلة على شكل التحويلات الهندسية؛ وذلك حتى يمكنك التعرف على الشكل الخاص بها:

خاتمة بحث عن الدوال الرئيسة الام والتحويلات الهندسية وامثله

بذلك نكون قد انتهينا من الإشارة إلى كل التفاصيل ذات الصلة بالعلاقة بين الدوال الرئيسة “الأم” والتحويلات الهندسية، حيث تضمن بحثنا الإشارة بتعريف كلًا منهما، إلى جانب تعريف المعنى المقصود من مصطلح العلاقة؛ باعتباره أحد المصطلحات الرياضية.

بالإضافة إلى ذلك فقد عرضنا بعض الأمثلة التوضيحية التي تربط بين كلاهما، وأشرنا إلى الأنواع الأكثر انتشارًا من تلك الدوال، ونشير في الختام إلى أن تلك المصطلحات هي أحد المصطلحات الرياضية التي لا غنى عنها عند دراسة هذا العلم.

اقرأ أيضًا: بحث رياضيات جاهز للطباعه متكامل العناصر

إلى هنا نكون قد قدمنا لكم نموذج بحث عن الدوال الرئيسة الام والتحويلات الهندسية وامثله على العناصر التي اشتمل عليها البحث الدراسي، ونتمنى أن نكون قد قدمنا لكم الإفادة المرجوة.